جست و جوی عمق اول (Depth First Serach)
DFS یکی دیگر از الگوریتم های پر کاربرد در پیمایش گراف است. DFS اولین مسیر lexicographical از ریشه (v) به هر راس دیگری در گراف را پیدا میکند.(اگر رئوس در گراف با یک یا چند حرف نامگذاری شده باشند ، آنگاه مسیر lexicographical ، مسیری است که رئوس به ترتیب دیکشنری طی شوند). همچنین DFS کوتاه ترین مسیر در درخت را نیز پیدا می کند ؛ برای اینکه در درخت فقط یک مسیر به هر راس وجود دارد ولی در گراف های دیگر از DFS به عنوان الگوریتمی برای یافتن کوتاه ترین مسیر استفاده نمی کنند. اردر این الگوریتم از (O(n+m است که n تعداد رئوس و m تعداد یال ها است.
توضیح الگوریتم
در واقع ایده های که در پشت DFS نهفته است این است که تا جایی که می توان در عمق گراف پیش رفت و وقتی به یک راس رسیدیم که هیچ همسایه دیده نشده ایی نداشت، به عقب بر می گردیم. الگوریتم به این شکل است که ابتدا ریشه (v) را انتخاب می کنیم و mark[v]=true می کنیم. سپس به یکی از همسایه های v مانند u که mark[u]=false است می رویم و همین الگوریتم را روی u و دیگر رئوس اجرا می کنیم. زمانی که به ازای راسی مانند u، تمام همسایه هایش را دیدیم به راس پدر ( راسس که از آن وارد u شده بودیم ) بر می گردیم و دوباره همین الگوریتم را اجرا می کنیم. برنامه زمانی تمام می شود که به راس ریشه (v) برگشته باشیم و به ازای هر همسایه v مانند mark[a]=true ، a باشد.
کاربرد ها
- پیدا کردن یک مسیر که از ریشه به رئوس دیگر می رود به ازای هر راس.
- پیدا کردن اولین مسیر lexicographical از ریشه به بقیه راس ها.
- چک کردن این که آیا یک راس جد یک سری راس دیگر در درخت است یا نه : زمان ورود به راس u را [starting time[u و زمانی که تمام همسایه های u را دیدیم و دوباره به u بازگشتیم (زمان خروج از u) را [finishing time[u می گویند. حال با این دو تعریف می توان برای هر دو راسی مانند (i,j) با (Order(1 می توان فهمید که کدام جد دیگری است و راس i جد راس j می باشد اگر و تنها اگر [st[i]<=st[j و [ft[i]>st[j باشد.
- پیدا کردن اولین جد مشترک دو راس در درخت به صورت آفلاین (LCA)
- مرتب سازی توپولوجیکال: در هر گراف جهت دار بدون دور ترتیبی از راس ها وجود دارد که در آن هر کس از همسایه هایش عقب تر است. واقع از Topological sort برای به دست آوردن finishing time های رئوس به ترتیب نزولی استفاده می شود.
- چک کردن این که گراف دور دارد یا نه و پیدا کردن دور آن : با شمردن Back edge ها در هر مولفه همبندی می توان وجود دور در گراف را پیدا کرد.
- پیدا کردن مولفه های قویا همبند در گراف جهت دار : ابتدا روی گراف Topol sort می زنیم بعد دنباله ایی از DFS ها را روی رئوس به ترتیبی که از Topol sort به دست آورده ایم ، اجرا می کنیم. برای هر DFS مولفه ایی که پیدا می کنیم ، مولفه قویا همبند نام دارد. مطالعه بیشتر
- پیدا کردن راس ها و یال های برشی
طبقه بندی یال ها در گراف
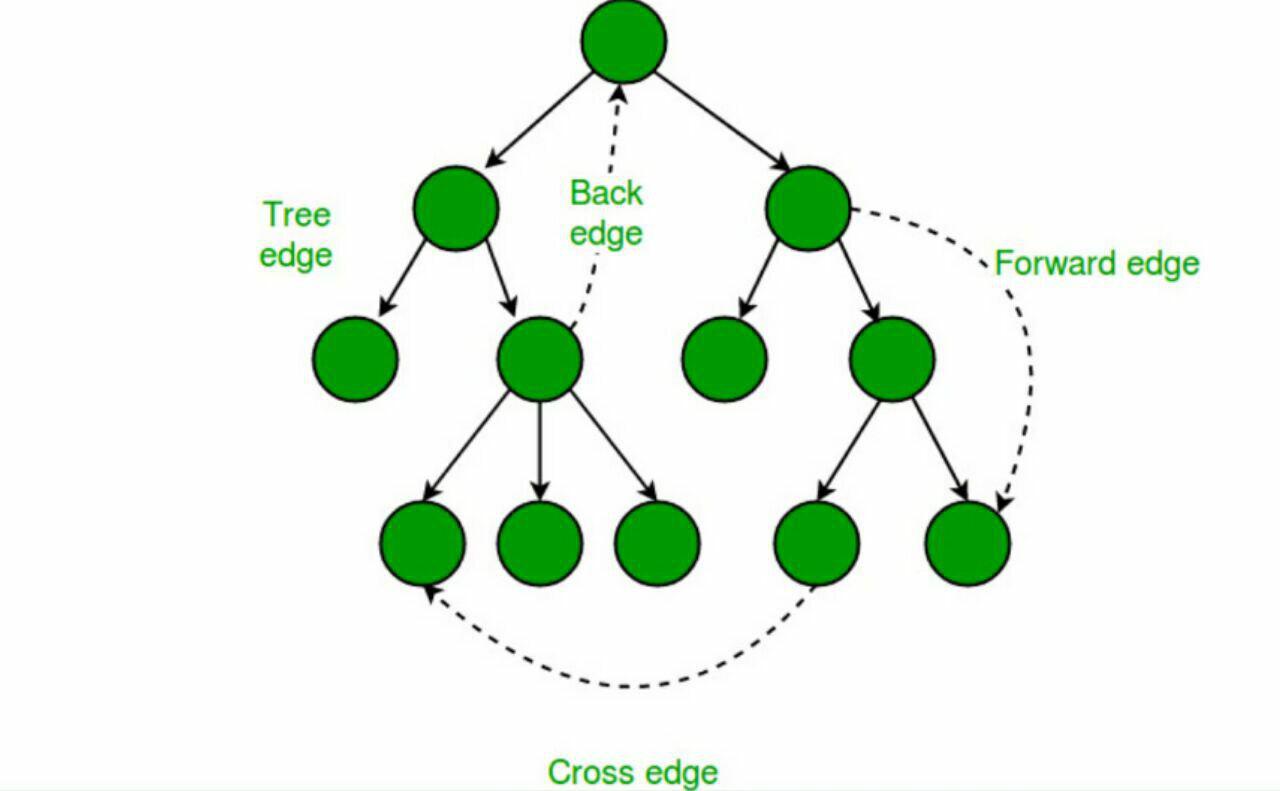
ما می توانیم یال های یک گراف را با توجه به starting time و finishing time دو سر یال (u,v) طبقه بندی کنیم. این طبقه بندی ها معمولا در حل کردن مسائلی چون پیدا کردن پل ها(Bridges) و یافتن راس های برشی استفاده می شود. در ابتدا DFS را روی گراف اجرا کرده و سپس یال هایی که با آن ها مواجه شدیم را این طور طبقه بندی می کنیم :
- اگر راس v دیده نشده بود: یال درختی -> اگر راس v بعد از راس u دیده شود آنگاه به یال (u,v) ، یال درختی می گویند. به عبارت دیگر اگر راس v برای اولین بار و بلافاصله بعد از راس u دیده بشود ، یال (u,v) درختی است، چون این یال در درخت DFS وجود دارد.
- اگر راس v قبل از راس u دیده شده بود: یال عقب رو (Back edge) -> اگر راس v جد راس u باشد آنگاه به یال (Back edge ، (u,v می گویند. در واقع این یال ها در گراف تشکیل دور می دهند چون قبلا توانسته بودیم از v به u برسیم و با این یال هم می توانیم از u به v برسیم. یال پیش رو(Forward edge) -> اگر v از نسل (بچه) راس u باشد، آنگاه به یال (Forward edge ، (u,v می گویند. در واقع اگر [st[u]<st[v باشد ، آنگاه v از بچه های u است. یال میانی (Cross edge) -> اگر v نه جد u باشد نه از نسل آن، آنگاه به یال (Cross edge (u,v می گویند. توجه : Cross edge ها و Forward edge ها فقط در گراف های جهت دار موجود هستند.
پیاده سازی
vector<vector<int>> adj; // graph represented as an adjacency list
int n; // number of vertices
vector<bool> visited;
void dfs(int v) {
visited[v] = true;
for (int u : adj[v]) {
if (!visited[u])
dfs(u);
}
}
این ساده ترین دی اف اس ممکن است. همان طور که در کاربرد ها صحبت کردیم، ممکن است محاسبه starting time یا چیز های دیگر مفید باشد. این پیاده سازی دی اف اس با محاسبه ی مقادیر کاربردی در بخش کاربرد هاست.
vector<vector<int>> adj; // graph represented as an adjacency list
int n; // number of vertices
vector<int> color;
vector<int> time_in, time_out;
int dfs_timer = 0;
void dfs(int v) {
time_in[v] = dfs_timer++;
color[v] = 1;
for (int u : adj[v])
if (color[u] == 0)
dfs(u);
color[v] = 2;
time_out[v] = dfs_timer;
}
مسائل تمرینی
- SPOJ: ABCPATH
- SPOJ: EAGLE1
- Codeforces: Kefa and Park
- Timus:Werewolf
- Timus:Penguin Avia
- Timus:Two Teams
- SPOJ - Ada and Island
- UVA 657 - The die is cast
- SPOJ - Sheep
- SPOJ - Path of the Rightenous Man
- SPOJ - Validate the Maze
- SPOJ - Ghosts having Fun
- Codeforces - Underground Lab
- DevSkills - Maze Tester
- DevSkills - Tourist
- Codeforces - Anton and Tree
- Codeforces - Transformation: From A to B
- Codeforces - One Way Reform
- Codeforces - Centroids
- Codeforces - Generate a String
- Codeforces - Broken Tree
- Codeforces - Dasha and Puzzle
- Codeforces - Making genome In Berland
- Codeforces - Road Improvement
- Codeforces - Garland
- Codeforces - Labeling Cities
- Codeforces - Send the Fool Futher!
- Codeforces - The tag Game
- Codeforces - Leha and Another game about graphs
- Codeforces - Shortest path problem
- Codeforces - Upgrading Tree
- Codeforces - From Y to Y
- Codeforces - Chemistry in Berland
- Codeforces - Wizards Tour
- Codeforces - Ring Road
- Codeforces - Mail Stamps
- Codeforces - Ant on the Tree
- SPOJ - Cactus
- SPOJ - Mixing Chemicals